Analogico Digitale: andata e ritorno - 3

di Mario Di Cola e Marta Furlan

Un bentornato a tutti. In questa puntata proveremo a compiere la difficile opera di persuasione nei confronti dei lettori più scettici cercando di convincerli che è effettivamente possibile ricostruire un segnale analogico a partire dai suoi campioni senza perdita di informazione. In questo modo avremo chiuso un primo cerchio e percorso il cammino di andata e ritorno dal mondo analogico al digitale, in attesa di addentrarci in aspetti più specifici legati alla pratica.

Campione per campione.

Immaginiamo di aver campionato il segnale analogico nel rispetto del teorema del campionamento: ciò che abbiamo così ottenuto è un "treno di impulsi", ovvero una sequenza di campioni equidistanziati; ciascuno di essi veicola l'informazione del valore puntuale del segnale analogico in un dato istante.

I valori puntuali di tensione in particolare sono stati "scelti" a intervalli regolari tra quelli infiniti possibili per il segnale di partenza. La seconda fase, la fase di quantizzazione, che consiste nella conversione dei valori in formato digitale, deve ancora avvenire. Nella pratica, una volta eseguita la fase di quantizzazione del segnale, avremo a disposizione sequenze finite di bit che rappresentano i diversi valori dei campioni a meno di una leggera approssimazione, … ma questa è un’altra storia e per ora la tralasciamo.

Torniamo al punto: vogliamo dimostrare che, a livello teorico, è effettivamente possibile ricostruire il segnale di partenza a partire dal suddetto treno di impulsi e che, se tutto va come deve andare, nel segnale ricostruito non manca proprio nulla di quello che era il segnale originale.

Se riconsideriamo l'ultima figura riportata nella scorsa puntata, sappiamo che lo spettro del segnale campionato è costituito da una serie infinita di repliche dello spettro del segnale originale, ciascuna centrata nei multipli della frequenza di campionamento. Il rispetto del teorema del campionamento assicura che tali repliche non siano sovrapposte l'una all’altra.

E se esaminiamo con attenzione tale situazione, potremmo pensare che per riottenere lo spettro del segnale originale sia sufficiente far passare il treno di impulsi attraverso un opportuno filtro passa-basso che "tagli" tutte le repliche successive lasciando solo quella a frequenza più bassa, che effettivamente coincide allo spettro del segnale analogico. Ci accorgiamo facilmente che questa strada è percorribile.

Realizziamo dunque la nostra intuizione e ipotizziamo di farlo a livello ideale: applichiamo al treno di impulsi un filtro passa-basso con caratteristiche ideali. Tale filtro, nella realtà solo approssimabile, presenta una caratteristica risposta in frequenza rettangolare, ovvero perfettamente costante ed unitaria in banda passante, con pendenza di taglio infinita ed enorme attenuazione fuori banda (cioè per frequenze superiori alla frequenza di taglio). Osservando la Figura 1 si vede innanzitutto che questa è un’idea valida. Inoltre, se fossimo nella condizione di sovrapposizione tra le repliche (ovvero in presenza di alias, ricordate?), incontreremmo serie difficoltà nel ricavare la banda originale.

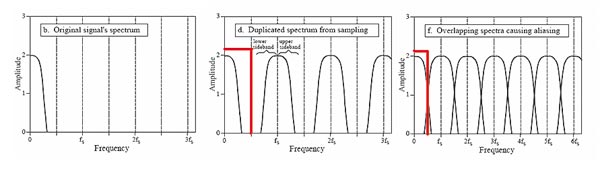
Possiamo convincerci che se avessimo a disposizione tale filtro potremmo ricostruire il segnale analogico in quanto la parte di spettro al di sotto della metà della frequenza di campionamento è identico a quello del segnale originale.

A che cosa corrisponde nel dominio del tempo questo filtraggio passa basso? Proviamo a vederlo, visualizzando l'andamento temporale dei segnali, in modo da focalizzarci su quello che è l'ambito più "immediato" per la nostra immaginazione: l'osservazione dei fenomeni nel tempo.

Immaginiamo, per ora, di far passare un solo impulso del treno attraverso il succitato filtro passa basso. Precisiamo che il segnale "impulso ideale" è, in sostanza, una variazione istantanea della tensione dal livello zero al livello massimo (positivo o negativo) e ritorno in un tempo infinitesimo.

Il singolo impulso ideale, una volta applicato il filtro passa-basso, si trasforma nel tempo come indicato in Figura 2.

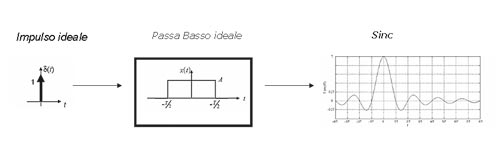
Facendo passare tale impulso attraverso il filtro passa-basso e osservando il segnale in uscita si osservano 3 cose importanti:

1.         la variazione di livello non accade più in un tempo infinitesimo, bensì compare una specie di "campana"

2.         compaiono delle ulteriori oscillazioni che tendono a smorzarsi nel tempo

3.         il segnale attraversa il livello zero a intervalli regolari

È come se il segnale che avevamo fosse stato "rallentato" da qualcosa perché non varia istantaneamente, ma ci mette "un po' di più"… la cosa non deve stupirci: ricordiamo che il segnale è passato attraverso un filtro passa basso che per sua natura ha l'effetto di attenuare tutte le componenti ad alta frequenza (leggi le sue componenti più veloci) lasciando passare solo le parte bassa dello spettro (cioè le componenti più lente).

Il segnale così ottenuto è detto "seno cardinale" o sinc ed è descritto matematicamente dalla seguente funzione: sinc(x) = sin (Tt)/ t, con T/2 banda (parte positiva) del filtro passa basso (supposto ideale, ovvero con guadagno unitario per tutte le frequenze)

In particolare esiste un legame ben preciso tra gli istanti in cui la funzione sinc assume valore zero e la banda del filtro passa basso che abbiamo applicato all'impulso. Tale legame risulterà importantissimo per la ricostruzione del segnale analogico col metodo del filtraggio passa basso.

Lo possiamo ricostruire…

Se ora noi facciamo passare il treno di impulsi attraverso il filtro, il risultato nel dominio del tempo sarà dato dalla somma di tutte le singole funzioni sinc derivate dal filtraggio di ogni singolo impulso.

Ciascuna funzione sinc:

1.         presenta valore massimo (altezza della campana) pari al valore di ampiezza del relativo impulso o campione

2.         presenta tale valore massimo posizionato nel tempo in corrispondenza del relativo campione

Tale filtraggio – nel dominio delle frequenze – si esprime matematicamente come moltiplicazione dello spettro del segnale di partenza per lo spettro del filtro. Il risultato corrisponde allo spettro del segnale filtrato.

Nel dominio del tempo invece, l'operazione di moltiplicazione degli spettri corrisponde ad un’operazione di "convoluzione" tra i corrispettivi segnali nel tempo.

I segnali che entrano nella convoluzione sono: il segnale campionato ed il segnale avente come spettro il filtro passa basso ideale, il quale ha banda “rettangolare”.

Sappiamo dunque 3 cose:

-abbiamo un filtro passa basso ideale, e sappiamo che ha banda passante pari alla (metà della) frequenza di campionamento

-sappiamo che questo corrisponde nel tempo ad una funzione sinc centrata nell'origine avente valori nulli nei multipli del periodo di campionamento, in sintesi che la funzione sinc è esattamente la risposta all’impulso di tale filtro;

-sappiamo infine che l'operazione di moltiplicazione nel dominio delle frequenze corrisponde ad una convoluzione nel dominio del tempo.

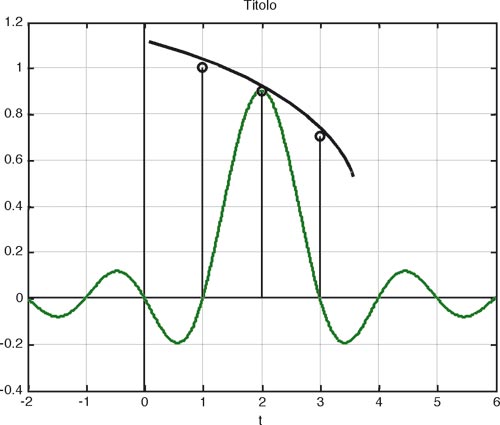
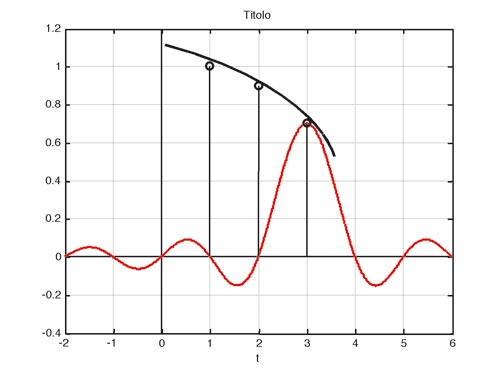
Il risultato della convoluzione è la somma dei risultati di infinite moltiplicazioni tra i due segnali. Ciascuna moltiplicazione è effettuata tra ciascuno degli impulsi formanti il treno di impulsi campionati e la funzione sinc (risposta nel tempo del filtro) ribaltata rispetto all'asse verticale e traslata di volta in volta di una quantità pari al periodo di campionamento. Poiché questa moltiplicazione fornisce ancora un sinc che viene solo scalato di livello dal valore del singolo campione ne viene che la funzione sinc risulta di volta in volta centrata esattamente in corrispondenza di uno dei campioni originari ed il suo valore massimo viene scalato da questi. Essa, ricordiamo, ha anche valori nulli in corrispondenza degli altri campioni.

Se sommiamo tutte queste funzioni sinc, ciascuna contribuirà a determinare il valore del singolo impulso essendo pesata in corrispondenza di esso, e darà un contributo nullo in corrispondenza degli altri. La loro somma pertanto darà, in corrispondenza di ciascun campione, il valore effettivo di ciascuno di essi. La Figura 3 espone graficamente quanto appena descritto.

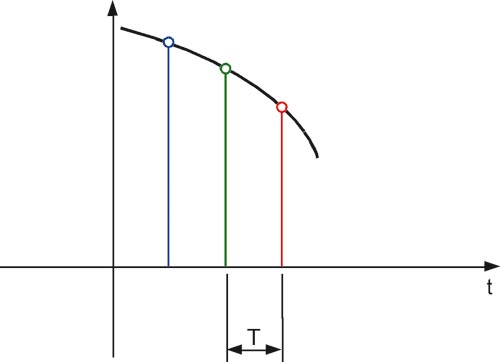
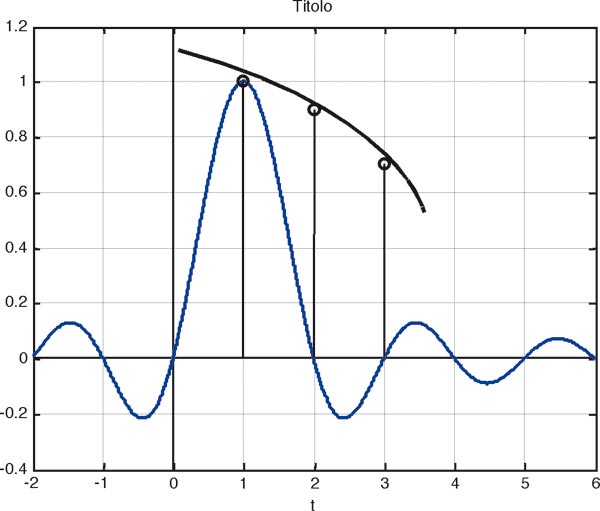
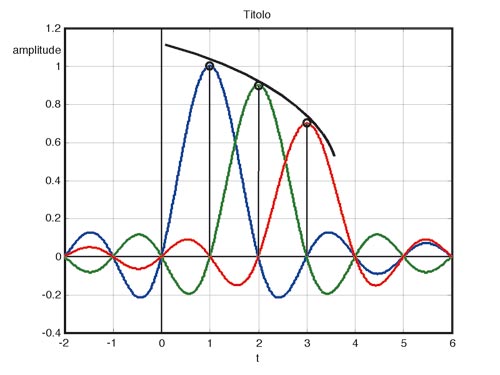
Cosa succede però nel tempo che intercorre tra l’arrivo di un campione e l’altro? Dobbiamo davvero credere di aver perso tutto?

No, perché ciò che l'operazione di convoluzione realizza è, in aggiunta, l'interpolazione tra i vari campioni.

La somma di convoluzione, infatti, genera valori non nulli tra un campione e l'altro determinati dalla somma pesata di tutte le moltiplicazione effettuate, raccordando così i valori discreti dei campioni con una "linea" che li unisce contenente gli infiniti valori del segnale analogico di partenza.

In sostanza si ha che il valore del segnale in uscita al filtro in ciascuno degli istanti in cui si riceve un campione da riconvertire corrisponde al valore vero e proprio che il campione ha. Poiché però questo campione è convoluto con un segnale sinc, si ha che per tutti gli altri istanti di tempo, diversi dagli istanti di campionamento, il valore dell’uscita viene dato dalla somma delle “code” di tutti i sinc prodotti dai campioni appena trascorsi e che continuano ad essere presenti sull’uscita per un po’ prima di smorzarsi del tutto. Quello che ne risulta per il segnale non è un andamento a caso o “tirato ad indovinare”. I vincoli di continuità e di contenuto spettrale di un segnale ci dicono che quello che abbiamo ricostruito è davvero il solo andamento che esso poteva avere, al solo patto di avere una banda limitata entro certi limiti che conosciamo (...e di cui abbiamo discusso).

Prima di lasciarci vorremmo riassumere una considerazione molto importante, tratta sempre dal libro di Stephen Smith, posta come opportuna conclusione di una spiegazione sul medesimo tema.

È necessario sfatare uno dei più importanti "falsi miti" che spesso osserviamo emergere con insistenza in occasione dei dibattiti sul tema analogico-digitale. Come sappiamo le informazioni contenute in un segnale digitale hanno, è vero, due tipi di limitazioni: il numero di bit per campione e la frequenza con cui sono presi i campioni. La prima può farci perdere informazioni su piccolissimi cambiamenti del segnale che possono perdersi nella quantizzazione. La seconda invece, limitando la risoluzione nel tempo del segnale campionato, potrebbe farci pensare che brevissimi eventi che accadono tra un campione e l’altro risultino persi per sempre. Questo fenomeno nel dominio della frequenza corrisponde alla necessità di "scartare" tutte le frequenze al di sopra della metà della frequenza di campionamento. (È vero che il Teorema del Campionamento dovrebbe assicurarci sul fatto che non abbiamo perso nulla del segnale originario ma tant'è: abbiamo la sensazione che un semplice Teorema non abbia tale forza di persuasione nei vostri confronti!)

Ecco qui il falso mito che ci tormenta: “Poiché i segnali analogici usano parametri continui essi hanno una infinita risoluzione sia nel tempo che nel livello del segnale stesso”.

Assolutamente falso! I segnali analogici sono limitati dagli stessi 2 problemi che limitano i segnali digitali: il rumore e la larghezza di banda.

Infatti come prima cosa il fenomeno della presenza di rumore in un segnale analogico limita la misura dell’ampiezza di una forma d’onda esattamente come la quantizzazione nel dominio digitale.

Inoltre, la capacità di distinguere due brevi eventi vicinissimi tra di loro nel tempo non è assoluta e illimitata ma dipende, anche nel mondo analogico, dalla massima frequenza riproducibile. Un segnale analogico limitato con precisione tra la DC e i 20kHz ha la stessa identica risoluzione nel tempo di un segnale campionato a 40kHz o poco più.

Quindi, a patto che il processo di campionamento sia realizzato a regola d’arte, tra un campione e l’altro non perdiamo proprio nulla.

Nella pratica, il processo di conversione Analogico-Digitale non è realizzato esattamente così, ma questa è l’idea che c’è dietro. Nella realtà infatti non è possibile ottenere un perfetto treno di impulsi per così dire "puntiformi" a valle del campionamento, né è possibile lavorare con esso. I tempi di elaborazione del segnale all'interno dei i vari circuiti fanno sì che un impulso di durata infinitesimale non sia lavorabile, poiché deve essere dato in pasto a dell'elettronica avente tempi di elaborazione finiti.

Nella pratica i circuiti che realizzano la conversione analogico-digitale mantengono il valore di ciascun campione fino a che non viene ricevuto il seguente.

Essi lavorano quindi su un segnale come quello indicato in Figura 4 realizzando un procedimento che si chiama ZOH che sta per "Zeroth Order Hold", cioè un mantenimento del valore del campione precedente "di ordine zero", in quanto di fatto realizzato con un linea costante che unisce i due campioni. Se avessimo voluto realizzare un simile processo di ordine uno, allora avremmo scelto una funzione che "interpola" i diversi campioni per mezzo di una retta; se fosse di ordine due per mezzo di una parabola ecc..

Di fatto è come se moltiplicassimo il treno d’impulsi per una serie di rettangoli realizzando nel dominio del tempo appunto lo ZOH.

Nel dominio delle frequenze l'operazione è l'inverso di quanto detto prima, in altre parole facciamo la convoluzione dello spettro. Focalizzandoci su ciò che accade alla replica centrata intorno allo zero, che è esattamente lo spettro del segnale di partenza analogico, vediamo che in seguito alla convoluzione essa si trasforma come da Figura 4.

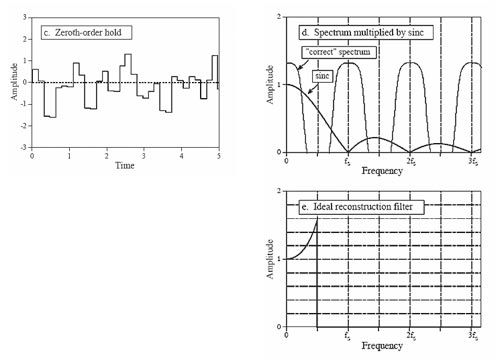
Il filtro ideale di ricostruzione è indicato sempre in Figura 4. Non sarà più un rettangolo ideale, ma qualcosa che compensi l'effetto della distorsione introdotta sullo spettro del segnale originale e dovuta al fatto che abbiamo utilizzato non un treno ideale d’impulsi ma un'interpolazione d’ordine zero.

Moltiplicando lo spettro della funzione campionata per tale filtro "modificato" possiamo così ottenere lo spettro iniziale e riconvertire il segnale. Di nuovo, tale moltiplicazione nelle frequenze, corrisponderà ad una convoluzione nel tempo, che questa volta sarà un convoluzione tra il treno di impulsi interpolato e la risposta all’impulso del filtro di ricostruzione. Poiché questo non è un rettangolo ideale, la sua risposta all’impulso non sarà più la funzione sinc, ma un'altra funzione più complessa.

Per ora ci salutiamo ben consci di aver lasciato più di una questione aperta sul tavolo. Torneremo a parlarne. Alla prossima!

CLICCA QUI PER ACCEDERE ALLA QUARTA PARTE