Analogico Digitale: andata e ritorno - 2

di Mario Di Cola e Marta Furlan

Come certo ricorderete, nella prima puntata abbiamo presentato la conversione analogico-digitale suddividendola per comodità in due fasi: “campionamento” e “quantizzazione” (traduzione in formato numerico). A dire il vero non è solo una questione di comodità, perché i convertitori in commercio sono effettivamente composti al loro interno da due dispositivi distinti che realizzano ciascuno una delle due fasi. Il campionamento è realizzato dai cosiddetti circuiti “Sample&Hold”, mentre la fase di quantizzazione è realizzata da dispositivi denominati “convertitori” o ADC.

In questa puntata approfondiremo meglio il modello teorico che descrive la prima fase attraverso la spiegazione del celeberrimo “teorema del campionamento”.

Questa insistenza sul modello teorico non è un tentativo da parte nostra di sedare il lettore, bensì un’operazione necessaria, un tributo che noi tutti dobbiamo pagare per capire come va condotta una conversione “a regola d’arte”.

In seguito infatti saremo in grado di affrontare la questione nella pratica per scoprire quali sono gli errori e il distaccamento modello-realtà che fa si che spesso le cose non si svolgano come scritto sulla carta.

Il teorema del campionamento

Questo importante teorema stabilisce la condizione necessaria affinché il segnale campionato sia ricostruibile a partire dai suoi campioni senza perdita di informazione.

Attenzione però! Il teorema del campionamento si riferisce esclusivamente a campionamenti effettuati ad intervalli regolari ed equi-distanziati: tale condizione è presupposto fondamentale alla buona riuscita del campionamento ed anzi come vedremo costituisce un requisito tecnico fondamentale, un benchmark nello stabilire la bontà di questa fase della conversione A/D. Quello che infatti andrebbe sottolineato, è che un audio digitale di ottima qualità prima che con tanti bit e con tanti campioni, si ottiene curando al massimo la stabilità della frequenza di campionamento in modo che tutti i campioni siano perfettamente equi-distanziati nel tempo.

La scorsa puntata abbiamo anticipato che "prendere i campioni significativi" significa conservare l’informazione veicolata dal segnale analogico anche dopo l’operazione di campionamento: se eseguiamo il campionamento in modo corretto saremo in grado di ricostruire esattamente il segnale analogico a partire dai suoi campioni. Ma come facciamo a “farci persuasi” (come direbbe Montalbano) che potremo ricostruire il segnale di partenza? Non è che magari tra un campione e l’altro succede comunque qualcosa di importante che ci perdiamo per sempre? Quali sono i criteri soddisfatti i quali siamo sicuri di aver portato a termine un campionamento corretto?

Una cosa alla volta. Pensiamo ad un segnale che varia lentamente nel tempo, al limite un segnale costante: ci convinciamo facilmente che basteranno pochi campioni per avere un’idea del suo andamento nell’insieme. Pensiamo ora ad un segnale che varia velocemente: in qualche modo intuiamo che di sicuro bisogna soffermarsi a fotografarlo “più spesso”, perché se prendessimo campioni troppo distanziati tra di loro, potrebbe accadere che il segnale vari in modo significativo proprio tra un campione e l’altro (ad esempio presentando improvvisi picchi), facendoci perdere informazioni importanti.

Ora, il nostro intuito ci dice che concetto di campionamento fatto “abbastanza spesso” coinvolge necessariamente il contenuto spettrale del segnale campionato e di conseguenza la frequenza di campionamento. Un segnale che contiene componenti ad alta frequenza andrà campionato più spesso rispetto ad un segnale che contiene solo componenti a bassa frequenza proprio perché il primo presenterà variazioni più rapide che non possiamo permetterci di perdere tra un campione e l’altro. Dunque, una volta individuata la banda necessaria per riprodurre con estrema fedeltà un segnale audio e quindi conoscendo la frequenza massima che dovremo campionare, il problema sarà uno solo: individuare la giusta frequenza di campionamento in modo da “catturare” bene anche i segnali alla frequenza di estremo banda.

Qual è il valore limite della frequenza di campionamento, che da ora in poi chiameremo fs, al di sotto della quale perdiamo informazione? Il teorema del campionamento afferma che se vogliamo che il segnale che campioniamo sia poi ricostruibile, due sono le condizioni che devono essere necessariamente soddisfatte:

il segnale da campionare deve avere banda limitata;

la fs dovrà essere pari o maggiore a due volte la frequenza massima contenuta nel segnale.

Queste due condizioni sono entrambe di importanza cruciale per far sì che il segnale campionato possa essere perfettamente ricostruito.

Soffermiamoci un attimo: il fatto che la banda del segnale debba essere limitata significa deve esistere un limite in frequenza al di sopra del quale tutte le componenti spettrali abbiano intensità nulla. In più, trovata questa frequenza massima, il teorema afferma che la fs deve essere almeno doppia di questa perché il campionamento possa essere realizzato con successo. Ad esempio: se dovessimo solo riprodurre il segnale di un basso elettrico, nel quale la frequenza massima sia, per ipotesi, intorno ai 2.000 Hz (ovvero la componente più "veloce" del segnale compie 2.000 cicli al secondo), la fs dovrà essere come minimo di 4.000 Hz, ossia dovranno essere presi almeno 4.000 campioni in un secondo.

Se però dobbiamo campionare con esso anche il segnale di un violino, che arrivi, ad esempio, fino a 15.000 Hz, sarà necessaria una fs di almeno 30.000 Hz, ossia si dovranno prendere almeno 30.000 misurazioni al secondo.

Nella pratica, in ragione del fatto che lo spettro dell'udibile per l'orecchio umano è compreso tra i 20 e i 20.000 Hz, una frequenza di 40.000 Hz dovrebbe essere il requisito minimo per campionare ogni possibile suono udibile dall'uomo.

In questa affermazione il condizionale è d'obbligo, perché i 40.000 Hz in realtà non sono altro che il “minimo sindacale”. Nella pratica purtroppo intervengono problematiche connaturate alla costruzione e al funzionamento dei dispositivi, per cui una fs di 44.100 Hz (lo standard dell’attuale CD), che è a tutt’oggi ancora molto usata, risulta essere il limite minimo reale per garantire una riproduzione ad alta fedeltà del segnale. Inoltre da molto tempo si è diffuso l’uso di una frequenza un po’ più alta, ovvero di 48.000 Hz, che rappresenta uno standard ancora largamente utilizzato nell’audio professionale, anche se è gia vasto l’impiego in vari tipi di apparecchiature dei 96 kHz e già si diffondono alcune macchine che lavorano a 192 kHz.

Consideriamo ora un singolo tono audio ideale, ovvero un segnale costituito da un’unica frequenza, una semplice sinusoide. Supponiamo di possedere un dispositivo che prenda, in un certo lasso di tempo, un certo numero di campioni del segnale: ad esempio, 14 campioni per periodo della sinusoide.

Otterremo una serie di campioni come quella in figura 1:

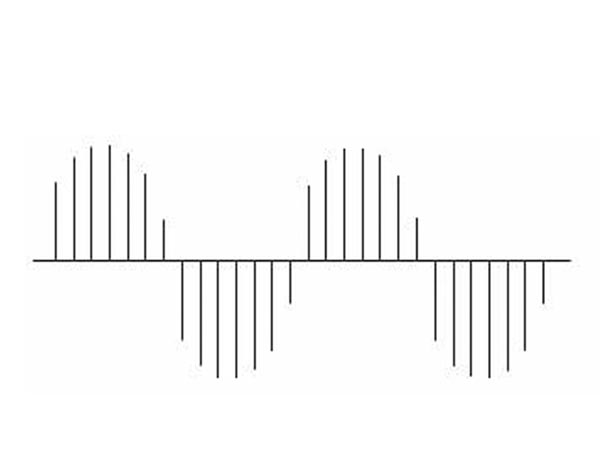
Figura 1: Una semplice sinusoide campionata 14 volte per periodo: ben riconoscibile.

Vediamo che la sinusoide originaria è perfettamente intuibile, per cui è possibile ricostruirla e invertire il procedimento. Immaginiamo ora di dimezzare la frequenza del campionamento prendendo 7 campioni per periodo, ossia di raddoppiare il tempo tra una misurazione e l'altra. Otterremo una diversa serie di campioni, meno fitta della precedente che vediamo in figura 2:

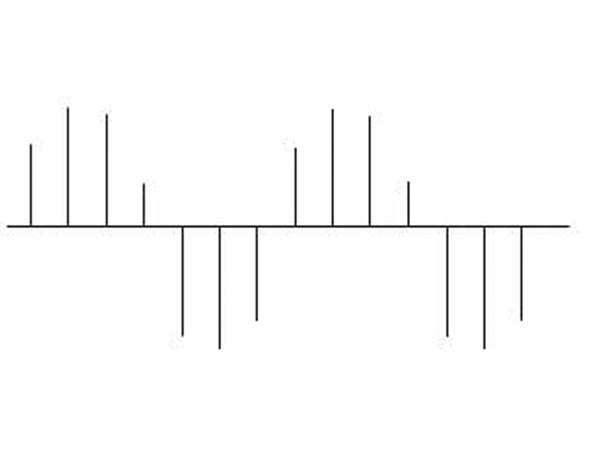
Figura 2: La stessa sinusoide campionata 7 volte per periodo: la scorgiamo ancora.

La sinusoide è ancora intuibile, ma è evidente che abbiamo perso alcuni dettagli dell’informazione, dettagli che da un punto di vista spettrale potevano anche essere del tutto insignificanti, vedremo meglio in che caso lo sono…

Dimezzando ancora e riducendo a 3,5 campioni per periodo, la situazione diventa quasi critica come in figura 3:

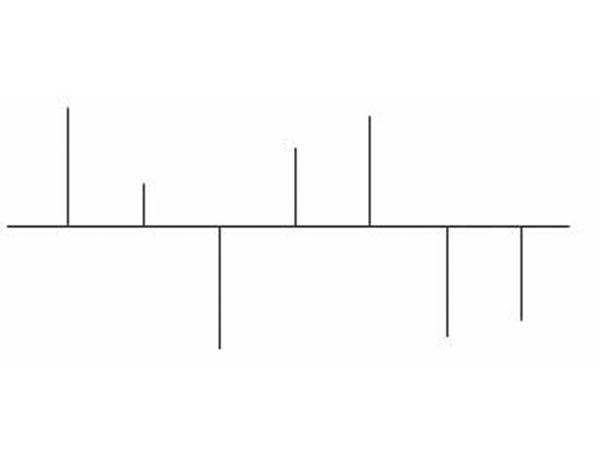
Figura 3: I campioni sono scesi a 3,5 per periodo: con un piccolo sforzo di immaginazione riconosciamo l’originale.

In ogni caso, anche se sembra strano, il segnale è ricostruibile. Dimezzando ulteriormente (1,75 campioni per periodo) come si vede in figura 4, si perde ogni traccia della sinusoide: in questo caso si è persa l’informazione, e quello che è ancora più bello è che ne è comparsa un’altra che prima era inesistente: un alias.

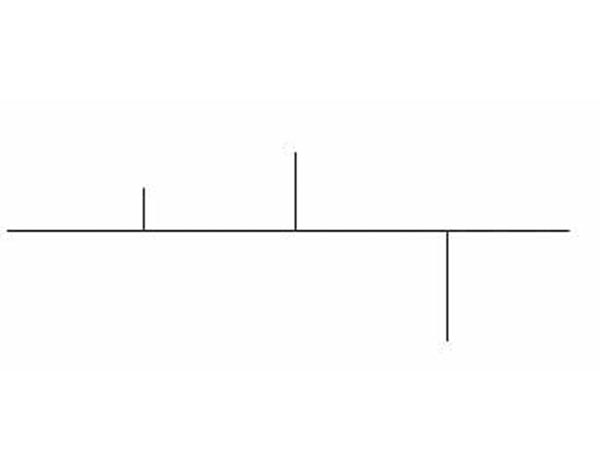
Figura 4: I campioni sono solo 1,75 per periodo:l’immaginazione non basta più!

In questo ultimo caso infatti non è stato rispettato il teorema del campionamento: la frequenza di campionamento era diventata troppo bassa per osservare con accuratezza il fenomeno. Infatti, dire che la frequenza di campionamento deve essere il doppio della massima frequenza del segnale significa – per segnali sinusoidali come quello dell’esempio – che bisogna prendere almeno 2 campioni per periodo per campionare correttamente. (Una semplice conseguenza del legame di proporzionalità inversa che sussiste tra frequenza e periodo di un segnale sinusoidale).

Del resto c’è anche da fare un’osservazione di buon senso: una sinusoide che si evolve nel tempo oscilla tra valori positivi e negativi. È ovvio (anche se non è scientifico spiegarlo così!) che per riconoscerla dovremo almeno beccarla un paio di volte nel suo periodo, così, tanto per sapere almeno che è stata “positiva” e che poi è stata anche “negativa”.

Difficile a credersi, con solo due campioni per periodo idealmente non c’è perdita di informazione! Siamo consci che questo fatto di “solo” due campioni per periodo può essere destabilizzante e destare perplessità: proviamo a “farcene persuasi” affrontando il tema anche da un altro punto di vista, ovvero curiosando nel dominio delle frequenze.

Il concetto di Alias

Chiediamoci ora: cosa accade se non rispettiamo il teorema del campionamento?

Quello che accade può essere visto da due punti di osservazione: nel dominio del tempo o nel dominio della frequenza; state però sicuri che significano la stessa cosa! Ciò che accade nel tempo tuttavia è un po’ più intuitivo di quello che accade nelle frequenze e quindi lo vediamo prima. Se si osserva con attenzione la sequenza dei quattro riquadri di figura 5, vediamo in maniera più raffinata quello che abbiamo gia dimostrato. Nell’esempio il numero dei campioni che prendiamo nell’unità di tempo è sempre lo stesso, ma la frequenza della sinusoide da campionare aumenta progressivamente. Unendo idealmente i campioni con una curva, la figura che ne viene fuori ricorda sempre meno la sinusoide di partenza. Nell’ultimo riquadro, la curva che li unisce individua addirittura una nuova sinusoide che non esisteva prima! Ecco l’alias. L’intruso indesiderato è comparso perché non abbiamo rispettato il teorema del campionamento.

Noi sappiamo bene che l’ultima sequenza di campioni così ottenuta è un alias perché abbiamo ben presente il segnale di partenza. Ma se questa sequenza per disgrazia giunge così com’è all’ingresso di un convertitore D/A ignaro di tutto, la forma d’onda che il convertitore ricostruisce è proprio quella “intrusa” che apparentemente emerge dai pochi campioni presi con conseguente perdita del segnale originale! Il danno è presto fatto. L’alias è riuscito a procurarsi un passaporto falso. E ora chi lo becca più?

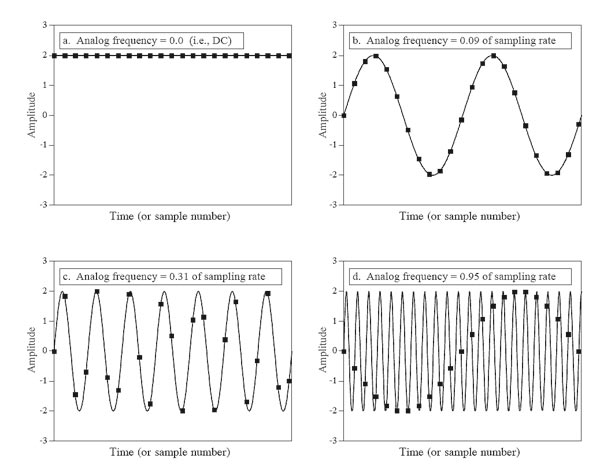
Figura 5: (tratta dal noto testo sui DSP di Steven W. Smith: The Scientist and Engineer’s Guide to DSP) I riquadri a) b) e c) mostrano un campionamento effettuato correttamente: i campioni identificano univocamente il segnale originale. Il riquadro d) invece mostra il fenomeno dell’aliasing: i campioni identificano una nuova forma d’onda che non corrisponde all’originale analogico.

Ma contemporaneamente a tutto ciò, cosa accade nel dominio della frequenza? L’azione di campionare il segnale ha un’importante conseguenza: lo spettro di ciò che otteniamo (che è anch’esso un segnale), la sua risposta in frequenza cioè, è data da un numero infinito di repliche dello spettro del segnale analogico originale, tutte distanziate l’una dall’altra di una distanza fs sull'asse delle frequenze (Figura 6 in alto).

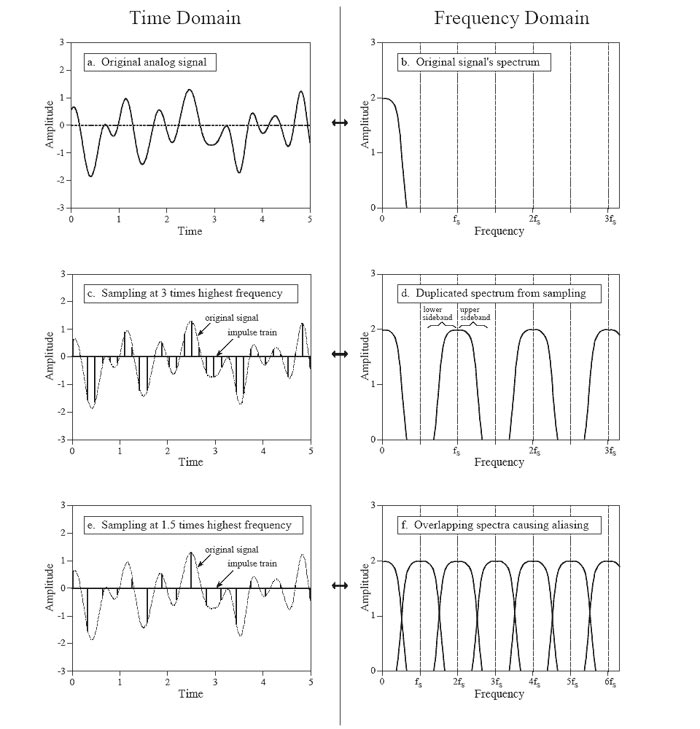
Attenzione: lo spettro del segnale originale non si estende solo da 0 Hz a 20 kHz ma c’è anche la parte negativa, quella che va cioè da 0 Hz a -20 kHz. No, pietà, non chiediamoci ora la spiegazione del perché di questo!

Se dunque fs non è almeno il doppio della banda, accade quello che potete vedere in basso nella Figura 6: sono causati errori nel segnale da ricostruire in conseguenza della sovrapposizione delle code nelle repliche spettrali del segnale originale campionato. Le code delle repliche si sovrappongono andandosi a sommare e generando uno spettro che purtroppo non corrisponde più a quello da cui eravamo partiti prima del campionamento. Si tratta di uno spettro “fantasma” (scusate il gioco di parole!), di un intruso che compare sotto falsa identità: è sempre lui, l’alias.

In conseguenza di ciò, quando campioniamo un segnale avendo scelto una opportuna fs, è buona norma limitarne la banda in ingresso al convertitore: in tal modo saremo assolutamente certi che in esso non siano presenti componenti significative per frequenze oltre fc=fs/2, (dove fc è il limite superiore della banda del segnale). È infatti una prassi consolidata inserire un filtro passa basso o filtro anti-alias prima del campionamento: grazie a tale filtro si evita la possibile sovrapposizione delle code il cui effetto genererebbe appunto l'errore di aliasing.

Figura 6: (tratta dal noto testo sui DSP di Steven W. Smith: The Scientist and Engineer’s Guide to DSP)L’operazione di campionamento nei due domini tempo e frequenza. Il alto, il segnale originale e relativo spettro. Al centro, un campionamento effettuato correttamente:le repliche spettrali del segnale campionato sono ben distanziate l’una dall’altra grazie all’elevato valore di fs e lo spettro originario è ben riconoscibile. In  basso, l'aliasing. Il valore di fs non è abbastanza elevato, le repliche si  sovrappongono e lo spettro risultante non ricorda più quello originario.  

L'adozione di questi filtri richiede particolare attenzione perché il loro impiego può causare distorsioni tali da compromettere in modo decisivo l'integrità del segnale in ingresso. Per ovviare a questi possibili problemi si suole spostare il più possibile verso l'alto la frequenza di campionamento, in modo da poter usare filtri più rispettosi dell'integrità dei segnali in ingresso. Così facendo, le distorsioni risiedono nelle zone a maggior frequenza, oltre la soglia di udibilità umana, e non alterano i suoni che noi interpretiamo come musica.

Proprio per risolvere questi problemi di distorsione e per ottenere sonorità più naturali, oggi si usano frequenze di campionamento altissime e i flussi digitali così ottenuti sono in seguito decimati per ricondurli entro i parametri standard dell'audio digitale memorizzabile su CD. In alternativa, è possibile registrare direttamente i dati numerici su DVD Audio oppure su SACD (Super Audio CD), che garantiscono una capienza e quindi una fedeltà sonora nettamente maggiori, e in questi casi si usano filtri passa basso estremamente semplici.

Bene, amici, con questo concludiamo la puntata. Tuttavia, pensiamo che ci sia ancora qualche lettore – forse più di uno – che non è ancora riuscito a “farsi persuaso” che si riesca davvero a ricostruire un segnale analogico a partire dai suoi campioni: cercheremo di convincerlo nelle prossime puntate!

CLICCA QUI PER ACCEDERE ALLA TERZA PARTE